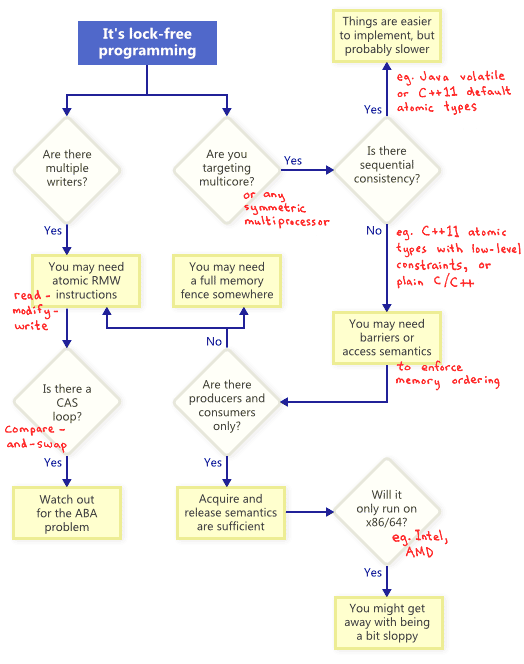
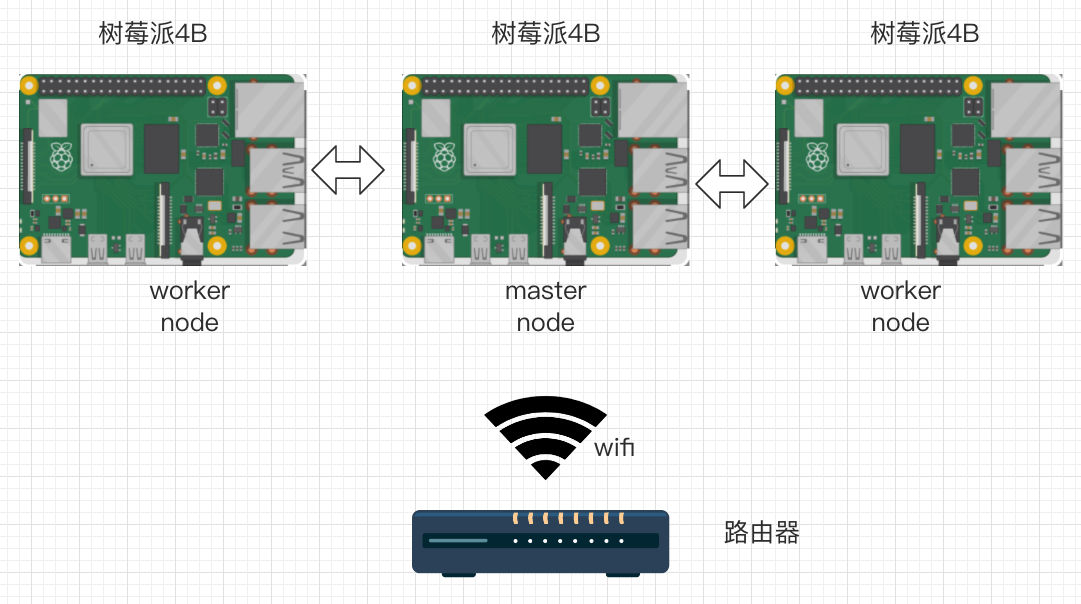
线性代数的本质

建立几何直观

我们在学校学习了如何进行矩阵运算, 熟练进行矩阵计算是基本功,但是你是否思考过, 为什么矩阵运算要这么定义, 矩阵运算是否有更加本质的意义.
对矩阵运算的算术意义的理解让我们能熟练使用矩阵工具来解决实际问题, 但是如果缺乏对计算的几何意义的理解, 当你要进一步深入解决问题的时候, 就会缺失问题解决的效率和灵活性.
打个比方, sin(x)的计算公式如下:

$$sin(x) = x - \frac{x^{3}}{3!} + \frac{x^{5}}{5!} - \frac{x^{7}}{7!} + ... + (-1)^{n-1}\frac{x^{2n-1}}{2n-1!}$$

于是任何x值,我们都能通过选择适当的n值来计算sin值. 如果我给你一个角度30度, 对应的弧度就是(𝝿/6)约等于0.5236, 于是你可以代入sin(x)的计算公式, sin(0.5236)=0.5236 - 0.0239 + 0.000328..., 结果约等于0.5. 这一切都符合预期.
但是如果我们知道sin(x)的几何意义: 在直角三角形中，一个锐角 ∠ A 的正弦定义为它的对边与斜边的比值，也就是：

$$sin(θ) = \frac{a}{c}$$

那么我们很容易通过绘制一个直角三角形并测量出sin()的近似值, 同时我们也很容易产生记忆, 30度角的sin值为0.5.这一切是建立在我们对计算公式产生几何关联的基础上,这种关联拓展了我们的解体思路,也加速我们的计算过程.
这种知识特性适用于各个方面, 他的层级结构如下:

(来自线性代数的本质-序言有的浏览器跳转后看不了请右键复制链接并粘帖到地址栏打开,下同!)

如果我们能掌握矩阵运算跟几何结构的关联, 那么就会对运算形成几何直观, 更好的掌握和使用他.

SOA框架iceoryx原理解析

简介

这篇文章，会介绍一个SOA框架，框架提供高效的通信能力。这个是他的logo，很漂亮，会让你忍不住想，这大概是个很酷的框架。

在我之前的一篇微服务的文章中曾经总结了微服务跟SOA的差异点和相同点，总结的结论如下：

1
2
3
4

差异可以归纳为：
SOA面向企业范围，微服务面向应用范围。
SOA带有异构集成的语义，微服务没有这个语义。
SOA服务内部支持组件分离的架构，微服务则是更彻底的组件分离架构-组件在网络上隔离。

基于这个总结，如果我们现在要写一套SOA服务框架，我们可以推导出这个框架的哪些特性呢？

从第一条中我们可以看出这套框架将是一个企业级别的框架，他不像微服务那样可以给每个服务灵活和独立的特性，SOA框架一旦推广使用，他就是企业级别的。

从第二条中我们可以看出，这个框架承担着异构集成的职责，异构集成简单讲就是适配加标准化公开这两点。展开来讲的话就是适配现有系统中的的专用数据格式、协议、传输机制，并使用标准化的机制将这些公开为服务。

从第三点上我们可以看出，这个框架所公开的服务，他们不一定像微服务那样一个服务与一个服务之间是网络隔离的，他们有可能是位于同一个主机上的，换句话说SOA的服务与服务之间可以网络隔离也可以网络不隔理。

这里面第一点可以认为是第二点的一个顺其自然的结果，由于各个服务都采用标准化的方式公开，那采用同一套框架是顺理成章的。所以下面我就只关注第二点和第三点。

这次要对其分析的这个框架叫iceoryx中文叫冰羚（其实就是对ice-oryx的翻译）。他是一个在特定领域（至少在智驾领域）很有名的SOA通信框架，在SOA特性的第二点和第三点特性中他都有很典型的体现，如下：

同步三要素

简介

在我之前写过一篇lockfree的文章，里面提到了CAS和内存屏障以及之间的关系，这里先总结一下。

lockfree主要是通过一定的编程规范来避免线程之间流程阻塞。不阻塞并不难，难的是不阻塞的基础上确保结果的正确性。

图中有两条重要的路线，一条是并发写，写的过程是一个Read-Modify-Write的过程，不是单步的，因此为了确保正确性，需要一个把RMW做成原子操作，于是CAS就出场了，这是一个处理器支持的操作，在汇编级别支持RMW原子性。

另一条线是多核指令顺序一致性，cpu为了性能，会做指令乱序，这种乱序在同一cpu的程序看来是感知不到的（cpu会自己保证这一点），但是会被其他cpu上的程序感知到，带来异常，为了消除这种乱序，我们需要使用经过封装的原子变量类型，或者使用内存屏障。如果要防止乱序的场景是一个线程写一个值，一个线程读一个值，那么我们通过acquire和release两个轻量屏障就可以实现了，别的场景有可能需要使用全能内存屏障，别的场景是什么呢？比如生产者生产的同时还消费，消费者消费的同时还生产，这就比较复杂，可能需要全能屏障来解决。

那么这两条路线的交集是什么呢，交集是多核执行RMW指令序列时，为了顺序一致性，除了要做到顺序一致，还需要保证结果正确。这个时候就需要CAS配合内存屏障了。

总结完之后，这一文，主要是要展开讲一下这里面更本质的东西，cpu乱序的本质是什么，内存屏障的本质是什么，cas的本质是什么，并延伸到锁的本质是什么。涉及到的技术主要是3点，包括：缓存一致性协议，内存屏障，锁。这三点可总结为同步三要素。

linux namespace

linux通过namespace技术为进程提供虚拟视图，这项技术是容器的基础。本文主要介绍每个namespace的实现原理，但很可能不对技术本身做探讨。比如会讨论如何实现cgroup的虚拟视图，但不会研究cgroup的控制器的实现原理。
目前在内核(v5.19-rc2,为写作之日的最新版本)中已经支持的namespace有8个。

1
2
3
4
5
6
7
8
9
10
11

https://github.com/torvalds/linux/blob/v5.19-rc2/include/linux/nsproxy.h#L31
uts namespace
ipc namespace
mnt namespace
pid namespace
net namespace
time namespace
cgroup namespace

https://github.com/torvalds/linux/blob/v5.19-rc2/include/linux/user_namespace.h#L66
user namespace

这些namespace起作用的场景是3个系统调用：

1. clone, 他接收namespace等参数，并完成fork进程的功能。
   https://man7.org/linux/man-pages/man2/clone.2.html
2. unshare,他创建新的namespace，并把本进程放到新namespace内。
   https://man7.org/linux/man-pages/man1/unshare.1.html
3. setns, 把当前进程加入到某些指定的namespace。
   https://man7.org/linux/man-pages/man2/setns.2.html

在分别讲每一个namespace之前，我们大致了解下内核代码的相关结构。

CKS知识总结

简介

CKS考试是kubernetes认证系列中中高级的一个证书，相比CKAD和CKA难度略大一些。

一方面虽然CKS跟CKA和CKAD有部分交集，比如k8s的基本使用，RBAC/secret的使用，集群升级等知识点，另一方面又是基于CKA的基础之上，考试也要求先通过CKA。

第二个相对难考的地方在于CKA和CKAD的考点都在kubernetes官网可以找到，但是CKS的很多知识点跳到了外部，涉及到外部的工具，外部的插件等等。

第三个点是CKS的部分知识点需要自己做一定的探索，换句话说不操作一遍的话都不知道他是什么，他涉及到什么知识。

同时，CKAD、CKA、CKS相同的点是都有前人为我们列好了考试大纲，列好了知识点和链接：CKA/CKAD/CKS

这里主要基于第3个难点，对涉及到的操作做一个细致的记录，方便大家参考，减少学习者的探索时间。

简介

挂载一个hostPath的volumes的时候，需要设置挂载方式为read only， 不然存在安全风险。

1
2
3
4
5
6
7
8
9
10
11
12

volumes:
- name: test-volume
  hostPath:
    path: /data
    type: Directory
这时定义hostpath的volume，定义的时候没有readonly选项。

volumeMounts:
- name: test-volume
  mountPath: /test-volume
  readOnly: true

在官方文档中有这么一段话

1
2
3
4
5

https://kubernetes.io/docs/concepts/storage/volumes/#hostpath

Warning:
HostPath volumes present many security risks, and it is a best practice to avoid the use of HostPaths when possible. When a HostPath volume must be used, it should be scoped to only the required file or directory, and mounted as ReadOnly.

简单讲就是在强调你在挂载hostpath的volume的时候必须设置readOnly，且必须约束可以挂载的目录。

设置readOnly是因为，已经证明存在一些方法来绕过约束。比如我配置了hostPath不能访问A目录，但是我可以通过挂载B目录间接访问A目录；或者我配置了hostPath只能访问A目录，但是我可以通过A目录，间接访问到B目录。是不是很神奇。

下面演示两个例子，来说明不设置readOnly和不约束可挂载目录所带来的隐患。

简介

k8s中内置了一种安全策略，能够用来约束pod的行为，他叫PodSecurityPolicy，位于apiserver中，默认被关闭。psp定义了哪些是能做的，他的作用范围大都是在securityContext这个结构中，其他也有，比如可以定义哪些volume是支持的，定义哪些端口是允许的。他通过限制这些结构来达到约束pod的目的。

但是psp是一个即将被废弃的功能，如果你看到文章的时候k8s的版本已经出到了v1.25了那么你可以不用看这部分了，根据官方文档，psp会在v1.25被彻底拿掉。至于psp的继任者Pod Security Admission我会在后续补上，当前我本地安装的k8s版本还不能使用，要v1.22才能使用。

1
2
3

https://kubernetes.io/docs/concepts/policy/pod-security-policy/

PodSecurityPolicy is deprecated as of Kubernetes v1.21, and will be removed in v1.25. It has been replaced by Pod Security Admission. 

我们来了解一下这个功能，并演示以下如何开启并使用他。

k8s中的危险权限

简介

本文列举了k8s中几个危险的权限，危险的权限是什么意思呢，就是说如果某个低权限的用户，因为其拥有某个特殊的权限，那么他就可以通过一些操作来提升自己的权限，从而破坏系统的权限控制体系，并产生意料之外的破坏，以及导致数据的泄露等。

这部分知识比较偏向攻击层面，而不是防守层面。我们通过一步步的手把手的操作，来观察如何突破权限，从而带来隐患的。

存在权限风险的操作主要有4个：bind，escalate，impersonate，create pod，我们一一来分析和测试。

存档k8s的证书

树莓派搭建k8s集群

简介

我们有很多时候需要搭建一个k8s集群，可能为了开发，可能为了测试，可能为了学习。在选择机器上可以有几个选择，一个是使用几台PC，一个是开几个虚拟机，一个是使用几个轻量的开发板。这里我主要以学习为目的，并且选择使用轻量开发板的方式，并且以最常用的树莓派作为代表，来搭建一个k8s集群。

由于主要以学习考试为主，这里暂时不考虑搭建单机集群的方式，因为没法接触到涉及多个节点的操作场景。

同时也不考虑k3s，我知道k3s是专为轻量设备而设计的，功能跟k8s基本是一样的，但是k3s和k8s只是功能基本相同，但是在使用和配置上，都有很多不同，并且使用的是完全分开的文档。k8s在使用上经常需要查在线文档的，即便对k3s的文档很熟悉了，在使用k8s的时候还是会存在查不到k8s文档的情况。因此学习k8s的时候，用k3s做练习是不合适的。

至于选择树莓派作为载体是个人选择，你可以选择使用pc或者选择使用虚拟机。如果你选择使用pc或者虚拟机，那么下面的章节中，【刷写系统】和【配置系统】会有差异，仅供参考。再之后的步骤则都是通用的。

最终我们将完成以下集群的搭建：

一个路由器，3个树莓派，树莓派通过wifi连接路由器，3个树莓派中一个master node,两个worker node。